1. DH算法简介
Diffie-Hellman密钥交换算法是在1976年由这两个人发明的算法。它可以在不安全的网络中,通过交换一些公开的信息协商出共享密钥,使用此共享密钥建立安全通讯。它实际上并没有直接交换密钥,而是通过数学计算,得出共享密钥。
有限域的离散对数问题的复杂度正是支撑DH密钥交换算法的基础。
DH算法属于非对称算法。DH算法专利已经与1997年到期。
它的原理很简单:
gamodp = A g^amodp=A gamodp=A
已知g,a,p求解A非常简单;而根据g,p,A在[1,p]范围内求解a却非常的困难,尤其当p特别大的时候(有多大?常见的DH组的p比特位有768,1024,2048,…, 8192,…)。放心吧,穷举不过来的!!!
2. DH算法协商流程
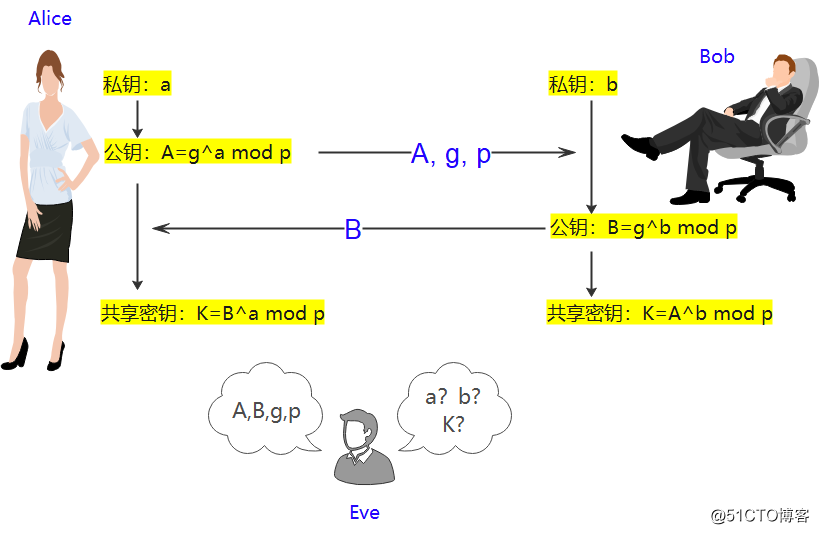
①Alice选择两个质数:p, g
p必须是一个非常大的质数,而g则是一个与p相关的数,成为生成元(Generator, 或数论中叫做本原根),g可以是一个比较小的数。
p, g是不需要保密的,即使被窃听也无关痛痒。
②Alice生成一个随机数a
a是一个位于1 ~ p-2之间的整数。这个数只能自己知道,不需要告诉Bob, 也不能让其他人知道。
③Alice计算出A
A = gamodp A=g^amodp A=gamodp
④Alice将p, g, A全部发送给Bob
这三个数可以让其他人知道,没有关系
⑤Bob生成一个随机数b
b是一个位于1 ~ p-2之间的整数。这个数只能自己知道,不需要告诉Alice, 也不能让其他人知道。
⑥Bob计算出B
Bob已经接收到Alice发来的g,p,因此可以计算出B。
B = g b m o d p B=g^bmodp B=gbmodp
⑦Bob只需要将B发送给Alice
B也可以让其他人知道,没有关系
⑧Alice利用Bob发来的B计算共享密钥K
K = Bamodp K=B^amodp K=Bamodp
⑨Bob利用Alice发来的A计算共享密钥K
K = Abmodp K=A^bmodp K=Abmodp
最后Alice和Bob计算出的共享密钥可以通过数学公式证明是同等的。因此通过DH密钥协商,最终双方协商出了只有两个人知道的共享密钥。DH算法数学原理上并不难,虽然大多数人在大学没有学过mod运算,看公式时一脸懵逼,总理解不到DH的精髓。事实上要证明此算法没有那么复杂。只需要二项式展开即可。
K = B a m o d p = ( g b m o d p ) m o d p = g a b m o d p = ( g a m o d p ) b m o d p = A b m o d p K=B^amodp=(g^bmodp)modp=g^{ab} modp=(g^amodp)^bmodp=A^bmodp K=Bamodp=(gbmodp)modp=gabmodp=(gamodp)bmodp=Abmodp
3. DH算法证明

4. SSL/TLS中的DH算法
DH算法分类标准有两类:第一种是基于密钥;第二类基于计算方式。
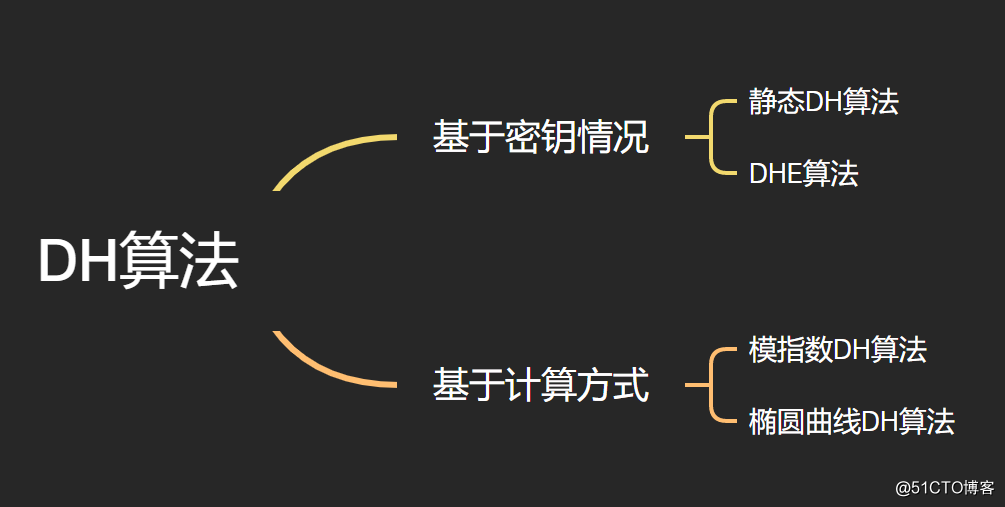
-
- 静态DH是指:通信双方有一方的私有密钥是固定的,另一方临时生成,一般是服务器端固定。但是这样随着时间的验证,很容易被破解,而一旦被破解,之前所有的通讯数据都很容易被解密,不具备前向安全的特性。目前静态DH基本不同。
- 既然静态DH算法中,一方固定一方临时生成的方式不安全,那么我们就双方都不固定。通讯双方的私有密钥都采用临时生成的方式,这中DH算法称之为DHE算法(E是指Ephemeral, 临时的)。
-
按照计算方式又可以分为:模指数DH算法和椭圆曲线DH算法。模指数是指:指数运算+取模运算,前面介绍的便是这种DH算法。但是这种算法由于涉及指数运算,计算量开销非常的可观,于是后来出现了椭圆曲线计算方式,据说这种方式计算量小了很多。
IPSec中的DH算法绝大多数是模指数DH算法,
SSL/TLS中采用的椭圆曲线DH算法。即ECDH算法
椭圆曲线DH算法称之为ECDH。 而模指数DH好像没有专业词,非专业的应该是MODPDH
DH算法是相当的逆天的存在。有一种:“看我不爽又干不掉我的样子”,我已经把信息都给你了,但是你却无能为力…。目前在做SSL卸载功能,它根本没有办法解析DH算法进行密钥配送的TLS协议,只能解析使用RSA进行密钥配送的协议。但是:现在大部分TLS都采用DH算法进行配送协商。SSL卸载功能对此几乎毫无办法。
转自:https://blog.51cto.com/u_13291771/3984396